算数の授業準備って大変です。
教材研究にも時間がかかるし、どうやって「教える」のか、わかりません。
そうですよね。
私も算数の授業準備には時間がかかっていました。
先日、「反転学習がいいよ」ということを耳にしてから、自分でも取り組んでみました。
反転学習…つまり、子どもに前もって「予習」してもらってから、授業に参加してもらう、ということですか?
その通りです。
事前に予習をしてもらってから授業に入ることで、私の教材研究の時間は大幅に減りました。
授業の質も高まり、子ども達も楽しく授業に参加できるようになったと思います。
また、「わかりやすく教える」という重圧からは、だいぶ解放されるかと思います。
面白そうです!
詳しく教えてください!
今日も一緒に考えていきましょう!

算数の授業準備が楽になる
まず、この記事は以下のような人に向けて書いています。
□ 算数の授業準備にかかる時間を減らしたい
□ 算数の授業がマンネリ化している
□ 「教える」以外の授業方法が知りたい
これらを解消するために「反転学習」を提案します。
私は1年生の担任なので、1年生の教室で実践してみました。
1年生で可能なので、基本的にはどの学年でも追試可能だと考えています。
反転学習の方法
前もって断っておきますが、反転学習について研究したわけではないので、詳しい理論は知りません(笑)。
とにかく、【予習→授業】という流れにしただけです。
まだ試行段階なので、はっきりとしたことは言えないのですが、第1時から導入するのはおそらく難しく、第3時あたりから導入するとスムーズかもしれません。
ただし、1年生以上の学年で、前学年で系統的に学んだ内容であれば、第1時からの反転学習も可能かもしれません。
1年生の場合は基本的に、「先行学習がない」という状態だと思いますので、「いきなり予習」というのは不親切かと感じました。
導入

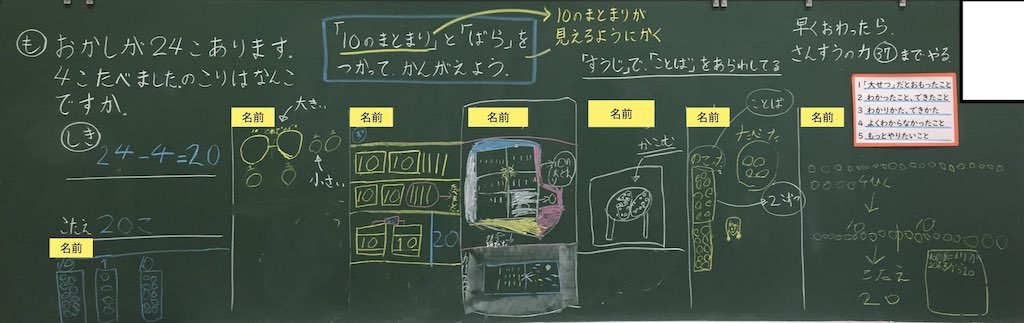
これは1年生「20より大きな数」の第5時くらいかと思います。
この日は訳あって時間がなく、20分ほどの授業でしたので、かなり駆け足で進めました…(ごめんなさい)。
左上の問題を、子どもに予習してきてもらいました。
授業前半のやりとりです。
自分で解いてみて、どうでしたか?
難しかった…
どうして難しいと思ったの?
「10のまとまり」じゃなかったから
いつもより「大きな数」だったから
なるほど。
では、今日は「どうやったら簡単にできるのか」を考えていくことにしますか。
反転授業の醍醐味はまさに「導入部分」だと思いました。
子どもは事前に問題を解いているので、すでに「問い(はてな)」が生まれている状態です。
ですから…
子どもの声から「めあて」をたてやすくなる
ただし、子どもの声をひろって「めあて」をたてることは、先生の大きな役割だと思っています。
子どもの声を上手くつなげて、本時の学習課題を見つけましょう。
展開
あとは、子ども達と一緒に
「どうやったら簡単にできるのか」
ということをひたすら探求していくだけです。
ここからは、「子どもが授業を進めてくれる」といっても過言ではありません。

まず、このように「0がついているもの」つまり「10のまとまりはやりやすい」という声を、共通確認しました。
「10のまとまり」に着目する考え方は、この単元では大切な「見方・考え方」だと思います。

次に、このように「十の位を手でかくす」という方法が出されました。
これだと一の位のみの計算になるので、簡単です。

「十の位と一の位の部屋を作って考える」という方法です。
これも、今後の学習で生かせそうな考え方です。
「一の位」を「ばら」と表現する考え方は、ここで出てきました。
これは教科書どおりではないでしょうか。

ここでは「一の位」を「一のまとまり」と表現しています。
「ばら」という表現と同じ意味ですが、子どもによってはこのような表現の方がわかりやすい子もいるようです。

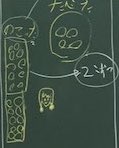
最後は、このように「手の指を使って考える」という方法です。
身近なモノを使って考える方法について、私は肯定派です。
「23に6を足す」ことを指を使って数えた、ということですね。
10以上を足す場合には使いづらくなりますが、具体物(指)を使って考えるという点では、1年生にとっては良い方法なのではないでしょうか。
まとめ
最後は、このカードの内容にそって、振り返りをしました。

このカードはかなり便利です。
事前に予習をした、反転学習の場合は…
□ 授業の初めに、この視点でたずねる
□ 授業の最後も、この視点で振り返る
というふうに使えます。
授業の前後で同じ質問をすることで、「ビフォーアフター」がよく見えます。
子ども自身も、授業の前後における、「自分の変化」に気付きやすくなります。
つまり、子どもが「学びを実感しやすい」ということです。
ちなみに、このカードの文言は、いつかどこかで目にしたものを活用しています。
どこで見たのだろう…
この視点を考えてくださった方、本当にありがとうございます。
すごく役に立っています。
次時の授業も紹介
次の授業でも同じように反転学習をしました。
この時間は45分の授業です。
先ほどのように、「めあて」は「子どもの声」からたてました。
問題を自分で解いてみて、どうでしたか?
昨日、「10のまとまり」と「ばら」を勉強したから、同じようにやれば、できたよ。
なるほど。
では今日は、「10のまとまりが見えるような絵をかく」ということを、やってみましょうか。
黒板の上の部分は「私が書いた」ものです。
下の部分は全て「子どもが書いた」ものです。
子ども達は、様々な方法で「10のまとまりが見える」ような絵をかいて説明をしました。
つまり、私が「めあて」を書いた後は、子ども達による「交流の時間」となるわけです。
黒板の前で、様々な考え方を交流していました。

数の大きさを「丸の大きさ」で表現しています。
量感にもつながる見方だと思います。

バラバラのものでも「10ずつ囲むと見やすい」という考え方です。
「2、4、6、8、10…」と、「2とび」で数えられるように並べると見やすい、という考え方です。

これは、子どもがよく使う「数え棒」を、そのまま絵にしたものです。
これ以外にも、様々な表現の方法を交流していました。
交流活動を通して、「数の操作」や「数の見方」について、子どもの声から、豊かに学べたのではないかと思いました。
終わりに
算数の授業を、「わかりやすく教える」方法を模索すると、途端に苦しくなってしまう先生もいるのではないでしょうか。
もちろん、「わかりやすく教える」ことができる先生は偉大なので、そのやり方も素晴らしいと思います。
私は「わかりやすく教える」ことが苦手なので、「子ども同士で教える」授業を提案したい、ということです。
反転学習の肝は…
□ 「問い」を引き出す「視点」を持っておくこと
□ 「めあて」を「子どもの声」からたてること
だと感じました。
まだ始めたばかりなので、なんとも言えませんが…。
「問いを引き出す視点」とは、記事の途中で紹介した「カードの視点」です。
「めあて」を「子どもの声」からたてることは、この授業で唯一、先生の腕が必要な部分です。
本時における「学習活動の視点になりそうな声」を、見つけてください。
焦らず、じっくり、ゆったり、子どもの声を聞いてから決めればいいと思います。















